We wrote kinetic equation for the average x as
![]()
| |
(6) |
We can speak only about average properties of f(t). We will
calculate ![]() and
and ![]() . We will average over
equilibrium ensemble.
. We will average over
equilibrium ensemble.
Averaging (6), we obtain:
![]()
| |
(7) |
| |
(8) |
![]()
But we know ![]() ! Result:
! Result:
![]()
![]()
![]()
![]()
![]()
![]()
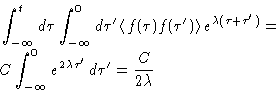
![]()
| |
(9) |
| |
(10) |
Sometimes the function f(t) is called random noise.
Equation (9) shows that random noise is
![]() -correlated. In other words, all harmonics are present in its
Fourier transform with equal weights
(equation (10)). Such noise is called
white noise (remember rainbow?).
-correlated. In other words, all harmonics are present in its
Fourier transform with equal weights
(equation (10)). Such noise is called
white noise (remember rainbow?).
Colored noise: not all harmonics are equal![]() :
:
![]()
How can it be so? What's wrong in our derivation?
| |
(11) |
Another interpretation: the ![]() -function in
equation (9) is the
-function in
equation (9) is the ![]() -function only
approximately. In fact it is a sharp peak with the width about the
characteristic time of the molecular processes.
-function only
approximately. In fact it is a sharp peak with the width about the
characteristic time of the molecular processes.
© 1997 Boris Veytsman and Michael Kotelyanskii